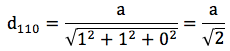Here is a mini lecture series on fracture in Turkish-still developing.
Henüz hazırlamakta (düzeltilmemiş) olduğum kopma ders notlarının bir kısmını paylaşıyorum. Her kesik çizgi arasında kalan alan bir konuyu temsil edecek şekildedir ve kendi içinde numaralandırılmıştır. Denklemler ‘D’ olarak gösterilmiştir. Malzeme bilimi üzerine Türkçe kaynak için lütfen muhendishane.org sitesine bakınız. Bu sayfanın içeriği CC BY-NC-SA 3.0 lisansı (Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License) ile lisanslanmıştır.
2012
İçerik:
1. Kopmaya genel bakış (Introduction to fracture)
- Kopmanın tarihçesi (History of fracture)
3. Teorik dayanım (Theoretical strength)
3.1. Teorik kesme dayanımı (Theoretical shear strength)
3.2. Teorik çekme dayanımı (Theoretical tensile strength)
- Gerilim konsantrasyonu (Stress concentration)
5. Griffith kopma teorisi (Griffith fracture theory)
6. Kopma tokluğu (Fracture toughness)
7. Gevrek kopma (Brittle fracture)
8. Sünek kopma (Ductile fracture)
9. Weibull istatistiği (Weibull statistics)
1.Kopmaya genel bakış
Kopma (fracture) malzemenin bir veya daha fazla parçaya ayrılması olarak tanımlanabilir. Hem günlük hayatımızı hem de yüksek teknoloji uygulamalarını doğrudan etkileyen kopma ne yazık ki her yıl dünya çapında binlerce ölüme ve milyarlarca zarara sebep olmaktadır. Bu yüzden kopma malzeme biliminin eskimeyen problemleri arasında yerini korumaktadır.
Bu bağlamda, kırılmanın tarihçesine kısa bir göz attıktan sonra, atomların birbirlerinden nasıl ayrıldığını ve teorik dayanımı (teorik strength) inceleyeceğiz. Daha sonra, malzemelerin içindeki küçük çatlakların nasıl gerilim konsantrasyonuna (stress concentration) sebep olduğunu, ve bu çatlakların Griffith çatlak teorisi ve gerilim yoğunluk faktörü (stress intensity factor) ile olan ilişkilerine bakacağız. Konunun devamında, genellikle seramikler ve camlarda görülen gevrek (brittle) kopmayı ve genellikle metallerde görülen sünek (ductile) kopmayı yakından inceleyeceğiz. Son olarak, endüstride ve akademide sıklıkla kullanılan Weibull kırılma istatistiğini anlamaya çalışacağız.
2. Kopmanın tarihçesi
İnsanlık tarihine bakıldığında kopmanın önemi daha iyi anlaşılır. Taş devrinden bu yana insanlar doğayı ve çevresini etkilemek için değişik malzemeler geliştirmiştir. Örnek olara
k 2.7-2.9 milyon yıl önce kullanılan sivriltilmiş taş aletler (1), M.Ö. 3000 yıllarında kullanılan bronz, ve M.Ö. 1300 yıllarında üretilmeye başlanan demir verilebilir. Bu malzemelerin yanında, kemik, deri, ve tahta gibi doğal malzemeler de tarih öncesi çağlardan günümüze halen kullanılmaktadır.
Kopma üzerine yapılan ilk yazılı araştırma Leonardo Da Vinci’nin (1452-1519) defterlerinde bulunmaktadır (2). Burada Leonardo demir tellerin kopma dayanımının tel uzunluğuyla ilişkisini deneysel olarak incelemiştir. Daha sonra Galileo Galilei (1564-1642) çekme ve bükme gerilimi altındaki kolonların kopmasını ¨İki yeni bilim üzerine diyaloglar¨ kitabında anlatmıştır (3). Bu noktadan sonra, modern kopma mekaniğinin (fracture mechanics) gelişmesi 300 yıl daha bekleyecektir.
Endüstri devriminin etkisiyle 19. yüzyılın ikinci yarısından sonra çelik kullanımı Bessemer yöntemiyle başlayarak devamlı yükselmiştir (4). Bu artış beraberinde çelik yapılarda güvenilirlik (reliability) sorunları da getirmiştir. Demir-çelik çekme dayanımı ve diğer özellikleri üzerine yapılan ilk kapsamlı araştırma 1864’de Kirkaldy tarafından yapılmıştır (5). Modern kopma mekaniğinin temelleri ise Griffith tarafından 1920’de yazılan makaleyle atılmıştır (6). Griffith kopmayı termodinamik temellere ve Inglis’in teorik gerilim konsantrasyonu hesaplarına (7) dayanarak açıklamıştır. Ama Griffith kopma teorisi sadece cam gibi gevrek (brittle) malzemelerin kopma dayanımını tahmin edebilmektedir. Bu teorinin metalleri de kapsaması yaklaşık 40 yıl sonra olmuştur.
İkinci Dünya Savaşıyla kaynaklı köprü ve gemi yapımı hız kazanmıştır. Kaynakla üretilen dört binin üzerinde Amerikan Liberty (özgürlük) kargo gemisinden bin iki yüzünün gövdesinde kopma meydana gelmiştir. Bu gemilerin 16 tanesi ise ortadan ikiye ayrılmıştır (8,9). Bu bağlamda, Amerikan Deniz Araştırma Laboratuvar’ında (U.S. NRL) çalışan Irwin Griffith kopma teorisini sünek (ductile) malzemeleri de kapsayacak şekilde genişletmesiyle kopma mekaniği günümüzde kullanılan halini almıştır. Sünek ve gevrek kopma arasındaki en büyük farkı yaratan plastik akma enerjisi artık Griffith kopma teorisine eklenmiştir (10). Irwin daha sonra Westergaard’in çatlak uçlarındaki gerilim hesaplamalarını (11) kullanarak gerilim yoğunluk faktörünü (K) tanımlamıştır:
Bu arada, σ malzemeye uygulanan gerilimi, Y geometrik faktörü, ve a yarı çatlak boyunu belirtmektedir (12). Yukarıdaki denklem metal, seramik, ve polimer gibi malzemeler için test edilmiş ve halen yaygın olarak kullanılmaktadır.
Referanslar:
(1) Rogers, Michael J., and Sileshi Semaw. “From nothing to something: the appearance and context of the earliest archaeological record.” In Sourcebook of Paleolithic Transitions, pp. 155-171. Springer New York, 2009.
(2) Leonardo da Vinci Codex Atlanticus 1504 Milano. In: Pinati, Milano, Bibilioteca Ambrosiana, 1894.
(3) Galilei G. Dialogues concerning two new sciences. Evanston, IL: University of Illinois Press; 1936, Trans. Crew H, De Salvico A.
(4) Ergun Türkcan , Dünya’da ve Türkiye’de Bilim, Teknoloji ve Politika, İstanbul Bilgi Üniversitesi Yayınları, 2009.
(5) Kirkaldy D. Results of an experimental inquiry into the tensile strength and other properties of various kinds of wrought-iron and steel. Glasgow; Private publication 1864.
(6) Griffith AA. The phenomenon of rupture and flow in solids. Phil Trans Roy Soc London 1920;A221:163–98.
(7) Inglis CE. Stresses in a plate due to the presence of cracks and sharp corners. Proc Inst Naval Arch 1913;55:219–30.
(8) F. Erdogan, Fracture mechanics, International Journal of Solids and Structures 2000;37:171–183.
(9) B. Cotterell, The past, present, and future of fracture mechanics, Engineering Fracture Mechanics 2000;69:533–553.
(10) Irwin GR. Onset of fast crack propagation in high strength steel and aluminium alloys. Proceedings of the Second Sagamore Ordinance Materials Conference 1956;2:289–305.
(11) Irwin GR. Analysis of stresses and strains near the end of a crack traversing a plate. J Appl Mech 1957;24:361–4.
(12) Westergaard HM. Bearing pressures and cracks. J Appl Mech 1939;6:49–53.
3.Teorik dayanım
Kopma için dışarıdan uygulanan gerilimin malzemeyi oluşturan atomları birbirinden ayrılması gerekir. Dolayısıyla bir malzemenin teorik dayanımı atom arası bağlara ve bu bağlara uygulanan gerilim türüne bağlıdır. Önce kesme gerilimi altında atom düzeyinde kopmayı inceleyeceğiz. Daha sonra aynı mantık ve biraz daha matematik yardımı ile çekme gerilimi altında teorik dayanımına bakacağız.
3.1.Teorik kesme dayanımı
Atomlar herhangi bir gerilim altında olmadıkça en karalı oldukları yerde dururlar. Bir atomu karalı olduğu yerden kaldırmak için atom arası bağların kopması gereklidir. Bu kopma için de yeterli enerji olmalıdır. Kısaca atomları rahatsız edecek derecede enerji yoksa atom arası bağlar kopmaz. Bu enerji kesme gerinimi olarak sağlanabilir.
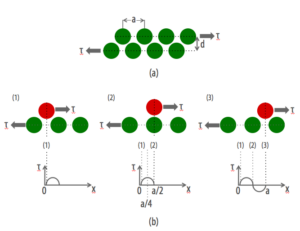
Şimdi kesme gerilimi altında atomların nasıl tepki gösterdiğini ve teorik kesme dayanımı bulmaya çalışalım. Öncelikle kesme gerilimini (τ) Şekil (a)’da görüldüğü gibi iki katmandan oluşan atomlara uygulayalım; atom arası uzaklık a ile, atomik düzlem uzaklığı d ile gösterilmiştir (1).
Atomlar kesme gerilimi altında kararlı oldukları yeri değiştirmemek için karşı gerilim gösterirler. Bu karşı gerilimin atom pozisyonuyla değişiminin sinüs fonksiyonu olduğunu varsayıyoruz. Şekil (b)’de kırmızı atomun sıfır direnç gösterdiği pozisyonlar 1, 2, ve 3 olarak belirtilmiştir. Bir ve üçüncü pozisyonda kırmızı atom kararlıdır. İkinci pozisyonda ise kırmızı ve yeşil atomlar üst üste geldiği için kırmızı atom kararsız durumdadır. Dolayısıyla, kesme geriliminin (τ) atom pozisyonuyla (x) değişimini aşağıdaki şekilde tanımlayabiliriz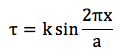 D1
D1
Bu fonksiyondaki tek bilinmeyen katsayı k’yi ise şu şekilde bulabiliriz. Küçük gerinim değerleri için sinüs fonksiyonun kendisine eşit olduğu varsayılır (sin(x)≈x).
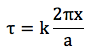
D2
Küçük gerinim için malzemenin elastik olduğunu kabul edebiliriz. Elastik malzemeler için:
![]() D3
D3
burada G kesme modülünü, x/d ise kesme gerinimini temsil etmektedir. İkinci ve üçüncü formülleri birbirine eşitlersek:
![]()
D4
Dördüncü denklemi de birinci denklemin içine koyalım:
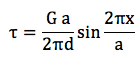
D5
Teorik kesme direncini bulmamız için kesme gerilimine en yüksek direnci gösteren pozisyonu bilmemiz gerekiyor. Kesme gerinimini sinüs fonksiyonu olarak kabul ettiğimiz için en yükse değere x=a/4’de ulaşılır, Şekil (b). Bu değeri beşinci denkleme koyarsak teorik kesme direncini buluruz:
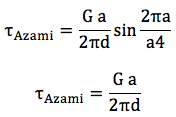
D6
Örnek olarak yüzey merkezli kübik yapıya bakalım. Bu tür kafes yapısı için a ve d arasındaki ilişkiyi aşağıdaki şekilde tanımlayabiliriz.
![]()
Bu değeri altıncı denkleme koyarsak yaklaşık teorik kesme dayanımını bulabiliriz:
![]()
Çeliğin kesme modülü yaklaşık 70 GPa’dır. Yani teorik kesme dayanımı 110 yönü için 70/4.5=15.6 GPa’dır. Bu değer genellikle MPa değerlerinde olan standart çekme test sonuçlarının çok üzerindedir ve bu çelişki dislokasyon teorisiyle açıklanmıştır.
Referans:
(1) J. Frenkel, Z. Phys., 37 (1926) 572.
3.2 Teorik çekme dayanımı
Teorik çekme dayanımı malzemenin dışarıdan uygulanan çekme gerilimine gösterdiği en yüksek direnci tanımlar. Ve bu direnç atom arası bağları koparmak için gereken gerilimle doğrudan bağlantılıdır. Teorik derken malzeme davranışının bizim tarafımızdan tanımladığını belirtiyoruz. Burada Orowan’ın varsaydığı gibi bir düzlemdeki atomların hepsinin aynı anda ayrıldığını ve atom arası kuvvetlerin yer değişimiyle (displacement) ilişkisinin sinüs fonksiyonu şeklinde olduğunu kabul ediyoruz (1).
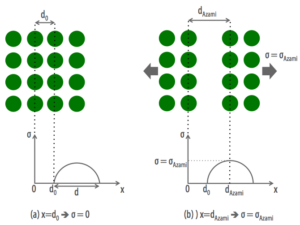
Atomlar gerilim altında karalı pozisyonlarından (Şekil a) ayrılırlar. Bu ayrılma sırasında atomlar dışarıdan uygulanan gerilime karşı bir gerilim gösterirler. Ancak azami karşı gerilim atom arası bağların el verdiği değeri geçemez. Şekil (b)’de görüldüğü gibi azami gerilime (σAzami) iki atom düzlemi arasındaki yer değişimi kopma noktasına (dAzami) gelince ulaşılır. Yukarıdaki şekilde malzemenin yönbağımşız (isotropic) ve yer değişiminin sadece iki düzlemde gerçekleştiğini varsayıyoruz. Gerilim ve yer değişimi arasındaki ilişkiyi aşağıdaki fonksiyonla tanımlayabiliriz.
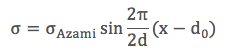
Burada σAzami ve d değerleri bilinmemektedir. Önce d değerini bulmaya çalışalım. Kopanın gerçekleşmesi için en az iki yeni yüzey oluşması gerekir. Bu yüzeylerin oluşumu için gereken enerji kopma esnasında açığa çıkar. Yani kopma sırasında yapılan bütün iş iki yeni yüzeyin oluşması için gereken enerjiye eşittir. Bu eşitlik tamamen gevrek malzemeler için geçerlidir.
Kopma esnasında her birim alan için yapılan iş Şekil (a)’daki eğrinin altında kalan alana eşittir. Bir eğrinin altındaki alanı entegral hesabıyla bulabiliyoruz. Şekildeki eğrileri sinüs fonksiyonu olarak tanımlamıştık. Şimdi bize entegral için üst ve alt limit gerekiyor. Entegralimizin alt limiti d0’dur. Üst limiti ise iki yüzeyin tamamen birbirinden ayrıldığı d0+d’dir.

Yukarıdaki entegralin çözümü için değişken değiştirme yöntemine başvurmamız gerekiyor. Eğer x-d0=y olarak kabul edersek, d(x- d0)=dy olur. Sabit değer olan d0’nun türevi sıfır olduğu için de dx=dy’dir. Bu durumda entegralimiz hesaplayabiliriz:
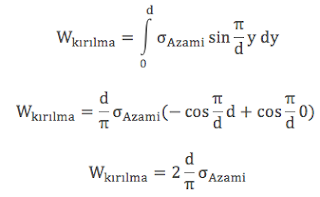
Bir birim alanı oluşturmak için gereken enerjiyi γ olarak kabul edersek, kırılma esnasında yapılan işi iki birim yüzey için gereken enerjiye eşitleyebiliriz.
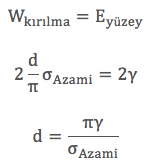
Teorik çekme dayanımını bulmak için d değerinin yanında σAzami de hesaplamamız gerekmektedir. Peki σAzami değerini nasıl bulabiliriz? Bunun için malzemenin küçük yer değişimleri için (x≈d0) Hooke kanununa göre davrandığını önceki konulardan hatırlayalım. Hooke kanunu gerilim ve gerinimin birbiriyle doğru orantılı olduğunu göstermektedir. Gerinimi yer değiştirmenin ilk uzunluğa oranı olarak gene önceki konularda görmüştük. Elimizdeki problem için sonsuz küçük (infinitesimal) gerinimi aşağıdaki şekilde tanımlayabiliriz:
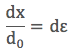
Bu gerinimi Young modülü tanımına eklersek aşağıdaki eşitliği elde ederiz.
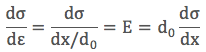
Birinci denklemde tanımladığımız gerilimin türevini alıp yukarıdaki denklemin içine koymaya çalışalım.

Sonsuz küçük yer değişimini x-d0≈0 olarak gösterilirse yukarıdaki kosinüs terimi bir olur. Bu durumda
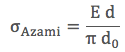
olur. İkinci denklemdeki d değerini üçüncü denkleme koyarsak, teorik çekme dayanımını buluruz.
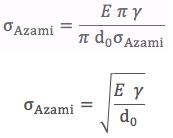
Dolayısıyla yüksek çekme dayanımı için yüksek yüzey enerjili ve birbirine yakın (küçük d) yüzeyler gereklidir.
Eğer d değerini d0‘ya eşit olarak kabul edersek yaklaşık teorik çekme değerini üçüncü denklemi kullanarak bulabiliriz.
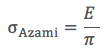
Örnek olarak çeliğin Young modülü 210 gigapaskaldır. Dördüncü denkleme kullanarak çeliğin teorik çekme dayanımı 67 GPa olarak buluruz. Bu değer çekme deney sonuçlarının çok üzerindedir. Standart testler çeliğin çekme dayanımının en fazla 2.5 GPa olduğunu gösterir.
Bu yüzden teorik dayanım değerleriyle laboratuvarda yapılan kopma test sonuçları arasında çelişki vardır. Bir sonraki konumuzda bu çelişkinin sebeplerini inceleyeceğiz.
Referans:
(1) E. Orowan, ‘‘Fracture and Strength of Solids,” Rep. Prog. Phys., 12 (1949) 185.
4. Gerilim konsantrasyonu
Önceki konularımızda teorik dayanımın malzemenin gerçek dayanımından çok daha yüksek olduğunu gördük. Teorik kesme dayanımın gerçek kesme dayanımından çok yüksek olmasını gerçekte malzemede dislokasyonların olmasıyla açıklandığını belirtmiştik. Peki teorik çekme dayanımının (yaklaşık E/π, GPa değerlerinde) gerçek çekme dayanımından (MPa değerlerinde) çok yüksek olmasını nasıl açıklayabiliriz?
İçinde çatlak bulunan bir bardağın kopmasının içinde çatlak bulunmayan bardağa göre daha kolay olduğunu hepimiz tecrübe etmişizdir. O zaman çatlağın kopmayı kolaylaştırdığını düşünebiliriz, bunu nitel (qualitative) bir gözlem olarak kabul edebiliriz. Peki, çatlağın kırılma üzerine olan etkisini nicel (quantitative) olarak nasıl gösterebiliriz? Bu problem Inglis tarafından çözülmüştür. Inglis elips şeklindeki çatlağın malzemede oluşturduğu gerilim konsantrasyonu aşağıdaki şekilde formüle etmiştir.
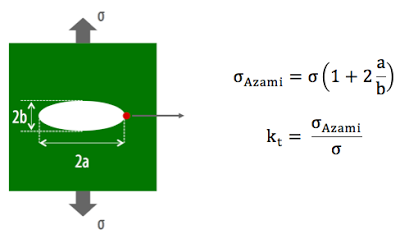
Elipsin asal (major) ekseni 2a, yedek (minor) ekseni 2b olarak kabul edelim. Yukarıdaki formülden anlaşılacağı gibi eğer malzemede uzun ve ince bir çatlak varsa, bu çatlağın önündeki azami gerilim malzemeye dışarıdan uygulanan gerilimden kat kat fazla olabilir. Gerilim konsantrasyonunu (kt) malzemenin içindeki azami gerilimin dışarıdan uygulanan gerilime oranı olarak tanımlıyoruz. Bu formülün ayrıntılı türetimi burada kullanmak istediğimizden fazla matematik içermektedir ama merak edenler iki ve üçüncü referanslara bakabilir.
Malzemede bulunan kesiklikler (discontinuity) gerilimi konsantre edebilirler. Bu kesiklikler genelde malzemenin içindeki çatlaklar (cracks) ve gözenekler (pores). Bu durumda teorik çekme değerine ulaşmak için malzemelerde çatlak ve boşluk olmaması gerekir. Gerçek çekme değerlerinin teorik değerlerden çok düşük olmasının ana sebebi de küçük çatlakların oluşturduğu gerilim konsantrasyonudur.
Eğer çatlak uzunluğuna göre çok ince ise (a>>b) gerilim konsantrasyonu eğrilik yarıçapı (ρ=b2/a, radius of curvature) cinsinden de gösterilebilir:
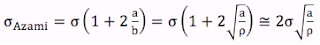
İkinci denklemde eğrilik yarıçapının gerilim konsantrasyonu üzerinde etkili olduğunu görüyoruz. Yani çatlağın veya boşluğun boyutlarından çok yapısı (form) gerilim konsantrasyonda etkilidir.
Referanslar:
(1) C. E. Inglis, Proc. Inst. Naval Arch., 55 (1913) 163, 219.
(2) J. F. Knott, Fundamentals of Fracture Mechanics, (London: Butterworths, 1973)
(3) K. J. Bowman, Introduction to Mechanical Behavior of Materials, Wiley, 2003.
5. Griffith kopma teorisi
Griffith kopmayı klasik mekanik ve termodinamik temellere dayanarak açıklamıştır (1). Cam üzerinde yaptığı deneylerle kopma problemini gerinim enerjisi ve yüzey enerjisi cinsinden tanımlamıştır. Bu tanıma göre var olan bir çatlağın ilerlemesiyle ortaya çıkacak gerinim enerjisi (elastic strain energy) oluşan iki yeni yüzey için gereken enerjiden (surface energy) fazlaysa kopma gerçekleşir. Bu durumda iki enerjinin çatlak uzunluğuyla değişimi bize kopma kriterini sağlar. Peki bu enerjileri nasıl hesaplayabiliriz?
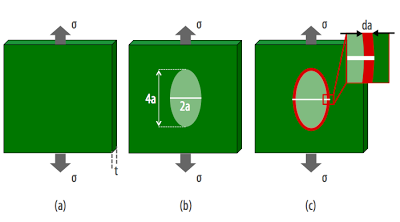
Öncelikle Şekil (a)’da görüldüğü gibi içinde çatlak bulunmayan bir malzemeye gerilim uygulandığı zaman oluşan elastik gerinim enerjisini hatırlayalım. Malzemenin eşyönlü (isotropic) ve Young modülünün E olduğunu varsayarsak, elastik gerinim enerjisi, U, gerilim-gerinim eğrisinin altında kalan alanın kalınlıkla (t) çarpımına eşittir:
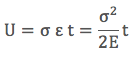
Gerilim altındaki bir malzemede biriken elastik gerinim enerjisini bulduk. Bu malzemede bir çatlak olursa elastik enerji düşer çünkü çatlak gerilimi iletemez. Ama ne kadar düşer? Bu sorunun yanıtını Şekil (b)’den yola çıkarak bulabiliriz. Şekil (b)’de ortada bulunan beyaz çizgi çatlağı temsil etmektedir. Bu çatlağın etrafında bulunan soluk alan ise çatlaktan dolayı oluşan gerilim rahatlamasını (stress relaxation) temsil etmektedir. Yani bu soluk alan içerisinde elastik gerinim enerjisi sıfırdır. Bu alanın elips şekilde olduğunu varsayarsak, rahatlama sonucu ortaya çıkan elastik gerinim enerjisini, UE, çatlak bulunmayan malzemenin elastik gerinim enerjisiyle elipsin alanını çarparak bulabiliriz. Elipsin asal eksenini 4a ve yedek eksenini 2a (çatlak uzunluğuna eşit) kabul edersek, elipsin alanı A:
olarak bulunur. Bu alanı elastik gerinim enerjisiyle çarparsak, rahatlama sonucu açığa çıkan elastik gerinim enerjisi, UE:
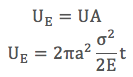
olur. Yani malzemede oluşan yada ilerleyen bir çatlak sonucu açığa elastik enerji çıkar. Şekil (c)’de çok küçük (da) çatlak ilerlemesiyle ortaya çıkan yeni alan kırmızı ile gösterilmiştir. Eğer açığa çıkan elastik enerji sadece yeni yüzeylerin oluşması için gereken enerjiye eşitse termodinamik denge sağlanır. Yeni yüzey enerjisini γS ile belirtirsek, kırılma ile ortaya çıkan iki yeni yüzey enerjisini, US, toplam çatlak alanı (2x2at) ve yüzey enerjisinin çarpımıyla buluruz.
Bu hesaplamalar sonucu elimizde elastik ve yüzey enerjileri mevcut bulunmakta. İçinde çatlak bulunan malzeme, Şekil (b), için toplam potansiyel enerji değişimini (ΔU) birim kalınlık için gösterebiliriz.
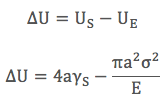
Çatlağın ilerlemesi sonucu açığa çıkan elastik enerji ve yeni çatlak yüzeylerinin oluşması için gereken enerji birbirlerine eşit olursa termodinamik denge sağlanmış olur. Termodinamik dengeyi ΔU’nun yarı çatlak uzunluğuna (a) göre türevini sıfıra eşitleyerek bulabiliriz.
Yukarıdaki denklemden belirli bir uzunluktaki çatlağı ilerletmek için gereken kritik gerilim (σk) değeri düzlemsel gerilim (plane stress) için bulunabilir.
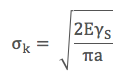
Düzlemsel gerinim (plane strain) altında çatlak ilerlemesi kalınlık yönünde kısıtlandığı için paydaya (1- ν2) eklememiz gerekiyor.
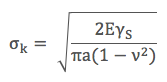
Referans:
(1) A. Griffith, “The Phenomena of Rupture and Flow,” Philos. Trans. R. Soc. London Ser. A 221, 163 (1921).
6. Kopma tokluğu (fracture toughness)
Önceki konularımızda teorik kopma dayanımından ve teorik değerlerin malzeme içinde bulunan çatlaklardan dolayı normalden çok daha düşük olduğunu gördük. İnce çatlakların malzemeye uygulanan gerilimi uçlarında konsantre ettiklerini de gördük. Çatlak ucunda oluşan yoğun gerilimin matematiksel tarifini Westergaard yapmıştır (1). Bu sayede çatlağın etrafındaki gerilim değerleri analitik formülle ifade edilmiştir. Daha sonra, Irwin bu sonuçları kullanarak modern kopma mekaniğinin (fracture mechanics) temellerini atmıştır (2).
Kopma tokluğu (KIc, fracture toughness) malzemenin kopmaya olan direncini tanımlayan bir özelliktir. Elastiklik teorisi (elasticity theory) belirli bir çatlak uzunluğu için kopmaya sebep olacak kritik gerilim değerini ise aşağıdaki formülle tanımlamıştır.
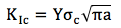
Yukarıdaki denklemde Y geometrik faktördür. Geometrik faktör çatlak geometrisi ve formu, malzeme geometrisi, ve uygulanan gerilim çeşidine dayanan birimsiz bir katsayıdır. Kritik kopma gerilimi σc olarak ve yarı çatlak uzunluğu a olarak temsil edilmektedir. Birimlere dikkat edecek olursanız, KIc’nin birimi sıradışı MPa√m’dir. Dolayısıyla kopma problemleri üzerine çalışırken birimleri daha dikkatli takip etmekte yarar var. Kopma malzemeye yüklenen (loading) kuvvet moduna göre üçe değişik şekilde gerçekleşebilir. Şekilde görüldüğü gibi Mod I açılmayı (çekme, tensile), Mod II kaydırmayı (sliding, shear), ve Mod III de yırtmayı (tearing, transverse shear) temsil etmektedir. Bunlardan Mod I en yaygın görülen kopma çeşididir. Kopma tokluğunda (KIc) görülen alt simge bu modu belirtmektedir.
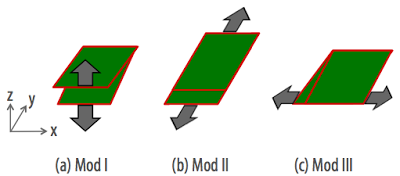
Denklem 1’i anlamak için bir örnek çözelim.
Aşağıdaki titanyum alaşımı (Ti-6Al-4V) bloğun kopma tokluğu KIc=55 MPa√m’dir. Toplam çatlak uzunluğu 2a=800 μm’dir. Bu bloğun dayanacağı azami gerilim nedir?
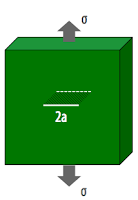
Denklem 1’i kullanalım.
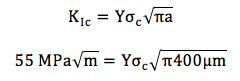
Burada, biri basit, iki sorunumuz var. Basit sorun çatlak uzunluğunun biriminin mikrometre olması ve bu birimin kopma tokluğu birimine uymamasıdır. Mikrometreyi metreye dönüştürmek için 10-6 ile çarpıyoruz.
İkinci sorun geometrik faktör Y’nin bilmemesidir. Çoğu değişik çatlak ve malzeme geometrisi için geometrik faktörler referans kitaplarda bulunabilir. Malzemenin kenarlarından uzak, iç (internal) çatlaklar için Y=1’dir. Bu durumda formülümüz.
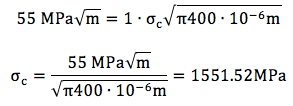
Yukarıdaki titanyum alaşım malzememiz içinde 800 μm (neredeyse 1mm) büyüklüğünde çatlak olmasına rağmen 1552 MPa gerilime kadar kopmayacaktır. Titanyum alaşım bu direnci yüksek kopma tokluğuna borçludur. Unutulmamalıdır ki seramik ve benzer gevrek malzemelerin kopma tokluğu genelde 5 MPa√m’den azdır.
Referanslar:
(1) H. M. Westergaard, J. Appl. Mechan., 5A (1939) 49.
(2) G. R. Irwin, J. Appl. Mechan., (1957) 24.
7. Gevrek kopma (Brittle fracture)
Kopmayı iki genel çeşit (gevrek ve sünek kopma) altında incelemeye çalışacağız. Gevrek kopmaya örnek malzemeler arasında cam, seramik, mineraller, bazı kompozitler, polimerler, ve soğuk metaller verilebilir. Şimdi diyeceksiniz ki neredeyse bütün malzemeleri saydın. Evet doğrudur. Neredeyse bütün malzemeleri şartlar elveriyor ise gevrek olarak kırabiliriz. Şartlar ile kastettiğimiz: gerilim, sıcaklık, gerinim hızı (strain rate), çevre, ve malzemenin üretim ve şekillendirme biçimidir (history of material). Gevrek kopma genelde malzemeler soğutulduğu zaman öne çıkar. Örnek olarak çikolatanın kopmasına bakalım. Günlük hayatımızda hoşlanmadığımız durumlardan biri güneş altında kalmış çikolatadır. Değil mi? Çünkü ısınan çikolata sünekleşir. Ama buzdolabına konan çikolatayı alıp rahatlıkla kırıp ikiye ayırabiliriz. Çünkü soğuk çikolatanın sünme (plastik akma) kabiliyeti düşük sıcaklıktan dolayı bastırılmıştır ve gevrek kopma gerçekleşir. Bu yüzden konumuzu oda sıcaklığında kopmayla sınırlıyoruz.
Kopma, genel olarak başlangıç (nucleation) ve ilerleme (propagation) aşamalarından oluşur. Önceki konularımızdan hatırlayacağınız üzere malzemelerin yüzeyinde ve iç yapılarında bulunan çatlak, gözenek, vb. hatalar gerilimi konsantre ederler. Bu durumda ince çatlaklar yüksek gerilimden dolayı ilerlemeye başlarlar. Eğer gerilim arttırıcı bir hata yoksa ki bu yalnızca çok ince fiber (whisker) gibi yapılarda görülür, kopma dayanımı teorik değerlere ulaşabilir. Bir çatlak ilerlemeye başlarsa genelde gevrek malzemeyi kırar çünkü kopma tokluğu dersinde gördüğümüz üzere çatlak uzunluğunun artması kopmayı kolaylaştırır. Bu yüzden gevrek malzemelerde kopma başlangıcı büyük önem taşır. Eğer gevrek malzemelerde kopma başlangıcını geciktirecek ve ya önleyecek bir yöntem bulursanız çok ünlü ve zengin olabilirsiniz.
Peki gevrek ve sünek kopma arasındaki fark nedir? En önemli fark gevrek kopmanın sünek kopmaya oranla çok daha düşük enerji gerektirmesidir. Sünek kopma esnasında çatlak etrafında yüzey oluşuna oranla çok daha fazla enerji gerektiren plastik akma gerçekleşir. Bu yüzden gerilim enerjisinin sadece atom arası bağların ayrılmasıyla oluşan kopmaya gevrek kopma diyoruz. Başka bir deyişle, kopma için gereken enerji malzemeyi en az iki parçaya ayıracak yüzeylerin oluşması için gereken enerjiye eşit veya çok yakın ise, bu gevrek kopmadır.
Seramiklerde gevrek kırılma en büyük problemlerden biridir. Temel malzeme bilgisi derslerinden hatırlayacağımız üzere seramik malzemeler kovalent veya iyonik atom arası bağlara sahiptirler. Bu yüzden plastik akma için gereken dislokasyonlar hareketsizdirler (sessile). Dolayısıyla seramik malzemeler elastik gerinim altında kopar.
Gevrek kopma malzemenin iç yapısına ve uygulanan gerilime göre değişik şekillerde gerçekleşebilir. Çekme gerilimi altında gevrek kopma iki genel grup altında gerçekleşebilir: tane arası (intergranular, Şekil (a)) ve tane içi (transgranular, Şekil (b)). Termodinamik olarak kopma en az enerji gerektiren yolda gerçekleşir. Eğer tane sınırlarının dayanımı tane içine göre düşükse kopma tane sınırlarında gerçekleşir, Şekil (a). Eğer tane sınırları kuvvetliyse kopma tane içinde en az direnç gösteren düzlemlerde gözlenir, Şekil (b). Cam gibi amorf malzemelerde tane sınırları olmadığı için bütün kopmalar tane içi olarak görülebilir.
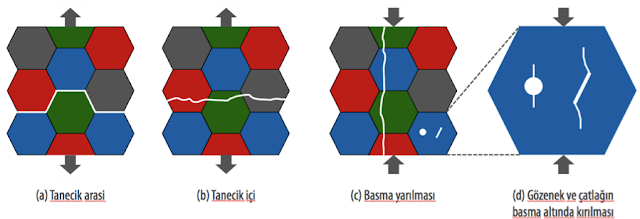
Çekme gerilimi altında zayıf olan seramikler basma gerilimi altında daha yüksek dayanım gösterirler. Yani kopma için gereken gerilim daha fazladır. Yakından tanıdığımız cam bardağın kırılganlığını biliyoruz. Magazin haberlerinden cam bardağın üzerinde çıkıp dans eden insanları görenlerimiz vardır. Genelde, basma gerilimi altında kırılgan malzemeler, basma gerilimine paralel doğrultuda ikiye ayırılırlar, Şekil (c). Bu ayrılmanın sebebi malzemenin içindeki çatlak ve gözeneklerin basma gerilimi altında dahi etraflarında çekme gerilimi oluşturabilmesidir. Örneğin Şekil (d)’de gözenekten basma gerilimine paralel ilerleyen çatlaklar görüyoruz. Bunun sebebi basma gerilimi altındaki gözeneğin alt ve üst kısımlarında çekme geriliminin oluşmasıdır. Şekil (d)’deki çatlağın ise uçlarında çekme gerilimi oluşur. Bu çekme gerilimi kanat (wing) çatlaklarını oluşturur ve kopma gerçekleşir.
8. Sünek kopma (Ductile fracture)
Sünek kopma, adından da anlaşılabildiği gibi malzemenin plastik akma olduktan sonra kopmasıdır. Bu plastik akmanın miktarı malzemenin çeşidine ve sıcaklığa göre değişir.
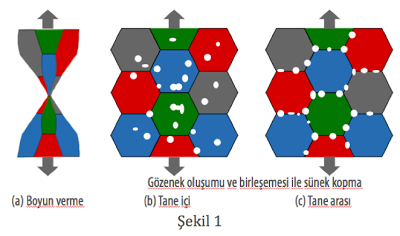
Çekme gerilimi altında çok sünek olan saf altın ve kurşun gibi malzemeler Şekil 1a’da görüldüğü gibi boyun vererek koparlar. Bu durumda çatlak veya kopmayı tetikleyecek gözenek gibi hatalar oluşmadan plastik şekil değiştirme devam eder ve malzeme incelerek ikiye ayırılır.
Metallerde en fazla gözlenen kopma biçimi ise gözenek oluşumu ve birleşmesiyle kopmadır. Eğer tane içi ve tane sınırlarının dayanımını birbirine yakın ise gözenekler malzemenin her yerinde oluşabilir, Şekil 1b. Eğer tane sınırlarının dayanımı tane içinden daha düşük ise gözenek oluşumu tane sınırlarında gerçekleşir, Şekil 1c. Gözenek oluşumun arkasında yatan en büyük nedenlerden biri malzeme içindeki yabancı fazlardır (inclusions).
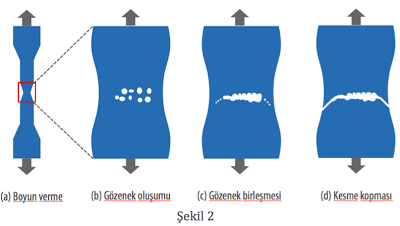
Şimdi, silindirik çekme numunelerinde sıklıkça görülen klasik çanak ve koni (cup-and-cone) kopma şeklini açıklamaya çalışalım. Çekme numunesi boyun vermeye başlayınca (Şekil 2a), boyun bölgesindeki gerçek gerilim seviyesi artar. Daha sonra boyunun iç kısımlarında gözenekler oluşmaya başlar, Şekil 2b. İç kısımdaki gözenekler gerilimin daha da artmasıyla birleşmeye başlarlar, Şekil 2c. Bu gözeneklerin arasında kalan bölgeyi küçük bir çekme numunesi gibi düşünebiliriz. Başka bir deyişle, gözenek arası bölgeler koparak gözenek birleşmesini sağlarlar. Dolayısıyla, numunenin orta kısmında oluşan çatlak etrafındaki gözeneklerle birleşerek büyür. Tek yönlü çekme gerilimi altında en yüksek kesme gerilimi 45 derecede oluşur. Bu yüzden silindirik numunenin çevresinde kalan alan son olarak kesme gerilimi altında yaklaşık 45 derecelik bir açıyla kopar, Şekil 2d. Bu şekilde gerçekleşen kopma sonucu numunenin bir tarafı çanak öbür tarafı koni şeklinde olur. Numunenin iç kısımları da gözenek birleşmesinden dolayı kenarlarına göre mat gözükür.
Atom seviyesinde düşünürsek, sünek kopma dislokasyonların hareket edebilme kabiliyetine bağlıdır. Yani metallerde dislokasyon hareketini kısıtlarsak gevrek kopma da görülebilir. Genelde sıcaklığın düşüşüyle metaller sünek kopmadan gevrek kopmaya geçerler. Bu olayı sünekten gevreğe geçiş olarak tanımlıyoruz. Bu geçişin oluştuğu sıcaklığa sünekten gevreğe geçiş sıcaklığı (ductilte-to-brittle transition temperature, DBTT) diyoruz.
Başka bir açıdan da oda sıcaklığında kırılgan olan cama bakalım. Normalde bir cam bir vazoyu yere atarsanız kırılır. Peki bu cam vazoyu cam üfleme tekniğiyle nasıl üretebiliyoruz? Tabiki ısıtarak. O zaman oda sıcaklığında kırılgan olan cam ısıtıldığı zaman sünek olabiliyor ve kırılmadan şekillendirilebiliyor. Bu ve benzeri kırılganlık değişimi bütün malzemeler için geçerlidir. Bu yüzden, her kırılma problemini dikkatlice tanımladıktan sonra incelemekte yarar var.
9. Weibull istatistiği
İstatistik de nerden çıktı kopma çalışırken derseniz bunun sebebi aynı şartlarda üretilmiş gevrek malzemelerin aynı koşullarda kırılma testine tabii tutulmalarına rağmen sabit değerlerde dayanım göstermemeleridir. Bu kavramı daha iyi anlamak için pencere camını kırılmasını bir göz atalım. Herhangi kırılma testi için önce numune hazırlamak gerekir. Bunun için boyutları büyük olan pencere camını 10 adet eş dikdörtgen parçalara bölelim. Takiben, numuneleri üç nokta bükme testiyle kıralım. Elde edilen 10 kopma dayanımına baktığımızda bu değerlerin birbirinden farklı olduğunu gözlemliyoruz. En iyi ihtimalle birbirine yakın değerler olur ama hiçbir zaman aynı olmazlar. Bunun sebebi de her malzemede buluna çatlak uzunluklarının farklı olmasıdır. Bu durumda özellikle kırılgan malzemelerde bir grup numunenin kopma değerleri tek bir rakamla belirtilemiyor. Kimisi yüksek kimisi düşük gerilim değerlerinde kopan malzemenin kopma dayanımını istatiksel olarak incelememiz gerekiyor.
Bu incelemenin öncüsü İsveçli mühendis Ernst Hjalmar Waloddi Weibull, 1939 yılında malzemelerin kırılma istatistiği üzerine ilk çalışmasını yayımlamıştır (1). Bu çalışmasında Prof. Weibull belirli bir malzemenin kırılma ihtimalini uygulanan gerilimle ve hacimle ilişkilendirmiştir. ‘Geniş uygulamalı bir istatistiksel dağılım fonksiyonu’ adındaki makalesinde çeliğin çekme dayanımından kül parçacıklarının boyutlarına değişik konularda geliştirdiği istatistiksel fonksiyonun kullanımı üzerine örnekler vermiştir (2). Günümüzde Weibull birikimli dağılım fonksiyonu (cumulative distribution functuion, CDF) iki veya üç değişkenli olarak kullanılmaktadır. Üç değişkenli Weibull dağılım fonksiyonunu aşağıdaki şekilde tanımlıyoruz.
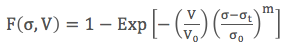
Burada F(σ,V) kopma ihtimalini, V malzemenin hacmini, V0 normalleştirme hacmini, σ homojen uygulanan çekme gerilimini, σt gerilim eşiğin, σ0 karakteristik dayanımı, ve m Weibull modülünü temsil etmektedir. Burada üç değişken σt , σ0, ve m’dir ve bu değişkenler Denklem 1’in bir grup test sonucuna oturmamız (fit) sonucu elde edilir. Konumuzu en basit haliyle anlatmak için gerilim eşiği bulunmayan iki değişkenli (σ0 ve m) Weibull birikimli dağılım fonksiyonunu üzerine yoğunlaşacağız:
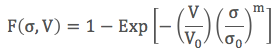
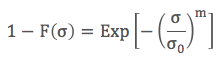
Her iki tarafın doğal logaritmasını alırsak:
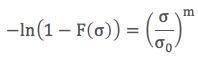
Her iki tarafın tekrar doğal logaritmasını alırsak:
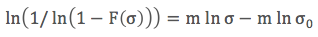
Denklem 5’in çizgiselliğini göstermek için sol tarafını y, ln σ değerini de x, ve (m ln σ0) terimini C olarak kabul edelim:
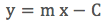
Denklem 6 bir çizginin denklemidir. O zaman üstel fonksiyonumuzu çizgiselleştirmişiz demektir.
Denklem 5’in Weibull grafiği üzerindeki gösterimini inceleyerek σ0 ve m değişkenlerini anlamaya çalışalım. Bunu konuya girişte verdiğimiz cam örneği üzerinden anlatmaya devam edelim. Elimizde 10 adet kopma testi sonucu var ve bunları Weibull grafiğinin içine koymaya çalışıyoruz. Bu değerleri önce artan şekilde sıralıyoruz. Bu sayede x eksenine koyacağımız ln σ değerlerini elde edeceğiz. Kopma ihtimalini içeren y ekseni için ise sıraladığımız kopma değerlerine kopma ihtimalini (Pk) kendimiz atıyoruz. Bunun için aşağıdaki formülü kullanıyoruz.
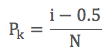
Burada i artan şekilde sıralanmış numune sırasını ve N toplam numune sayısını belirmektedir. Örneğimizde N=10’dur. Kopma ihtimalini i yerine 1’den 10’a kadar tam sayıları koyarak Pk’yi hesaplıyoruz. Bu Pk değerini ln(σ) yerine koyup y eksenindeki değerleri ln(1/ln(1-F(σ))) formülünden elde ediyoruz. Tablo 1’de bütün değerlerimizi toplu şekilde görebiliriz. Buradan aldığımız x ve y değerleriyle oluşturduğumuz Weibull grafiğini çizgisel bir görünüm sergilemektedir.
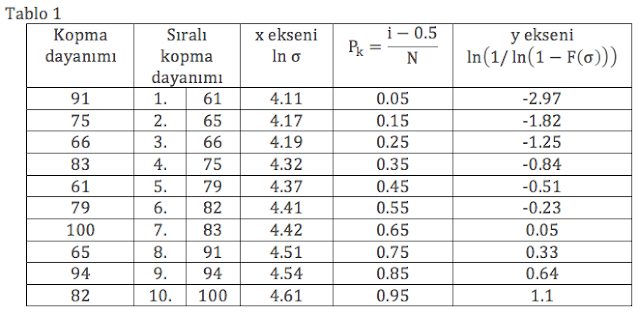
Weibull grafiği genelde kopma değerlerini ve bu değerlere oturtulmuş iki değişkenli Weibull dağılım fonksiyonunu içerir. Peki iki değişkenimizi Weibull modülünü (m) ve karakteristik dayanımı (σ0) nasıl hesaplayabiliriz. Bu değişkenleri en kolay doğrusal bağlama (linear regression) yöntemiyle bulabiliriz. Bunun için x ve y değerlerini herhangi bir hesaplama programına koyup bir çizgi denklemi (6. denkleme benzeyen) alabiliriz. Bu çizgiyi (y = -31.43 + 7.07 x) Weibull grafiğinde yeşil renkte görüyoruz. Çizgi denklemimizin eğimi (yani x’in önündeki katsayı) Weibull modülüne ~7 eşittir. Bu denklemin sıfıra eşit olduğu (y=0) nokta ise karakteristik dayanımı verir. Kısaca x=31.43/7.07=4.49, burada x değerinin gerilimin doğal logaritması olduğunu hatırlarsak, gerilim değeri aslında e4.45≅85 MPa’dır. Bu nokta Weibull grafiğinde yeşil çizginin y=0 çizgisiyle kesişimdir.
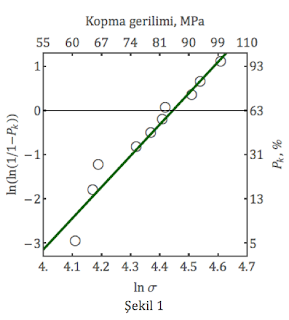
Weibull modülü ve karakteristik dayanımı daha iyi anlamak için Şekil 2’de iki farklı kopma verisine inceleyelim. Şekil 2’de yeşil çizgi çember ve kırmızı çizgi üçgen ile gösterilmiş kopma verisine oturtulmuştur. Yeşil çizginin değişkenleri m=7 ve σ0=83 MPa’dır, kırmızı çizginin ise üçgen m=15 ve σ0=99 MPa’dır. Peki karakteristik dayanımın çember veriler için üçgen veriye oranla daha düşük olması ne anlama geliyor? Şekil 2’de y=0 çizgisi aynı zamanda Pk=63% kopma ihtimalini göstermektedir (sağ eksen). Bu demektir ki çember verinin elde edildiği malzeme 83MPa gerilim altında 63% ihtimalle kopar. Üçgen malzeme ise daha yüksek 99MPa gerilim altında 63% ihtimalle kopar.
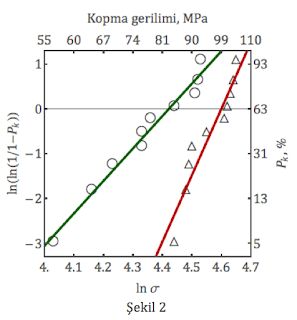
Weibull modülünün yüksek veya düşük olması bize kopma verisinin ne kadar dağınık olduğunu gösterir. Şekil 2’de üçgen veriler için m=15’dir, çember veriler için ise m=7’dir. Bunun sebebi çember verilerin daha geniş bir aralıkta-[56, 93]MPa-ve üçgen verinin ise daha dar bir aralıkta-[85, 105]MPa-kopma dayanımı göstermeleridir. Weibull modülü yükseldikçe malzeme de daha güvenilir (reliable) olur. Örnek olarak 80MPa gerilim altında malzemenizin kopma ihtimalinin yüzde 5’ten düşük olmasını istiyorsanız üçgen verinin elde edildiği malzemeyi tercih edersiniz.
Referanslar:
(1) W. Weibull, “A Statistical Theory of the Strength of Materials,” Ing. Vetenskaps Akad. Handl. (Roy. Swedish Inst. Eng. Research Proc.), NR 151 (1939)
(2) Weibull W. A statistical distribution function of wide applicability. J Appl Mech 1951:18.” 293-297